Étendue (max – min), variance, et écart-type

Les étendue, variance et écart-type sont des mesures de dispersion en statistiques descriptives. Elles permettent de quantifier à quel point les données d’un ensemble sont dispersées ou concentrées autour d’une valeur centrale (comme la moyenne). Voici une explication détaillée de chacune :

1. Étendue (Range : max - min)

• Définition : L’étendue est la différence entre la valeur maximale et la valeur minimale d’un ensemble de données. Elle donne une idée simple de l’amplitude totale des données.
• Formule : Eˊtendue=valeur maximale−valeur minimale\text{Étendue} = \text{valeur maximale} - \text{valeurminimale}Eˊtendue=valeur maximale−valeur minimale

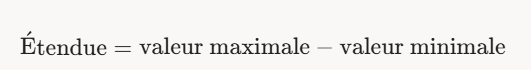
• Exemple : Pour les données 5, 8, 12, 15, 20 :  Etendue=20−5=15

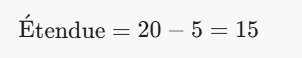
• Utilité :
• Mesure rapide et intuitive de la dispersion.
• Utile pour comparer des ensembles (ex. températures maximales et minimales sur une journée).
• Limites :
• Ne prend en compte que les deux valeurs extrêmes, ignorant la répartition des autres données.
• Très sensible aux outliers (valeurs aberrantes). Exemple : Si on ajoute 100, l’étendue passe à 95, sans refléter la majorité des données.

2. Variance

• Définition : La variance mesure la dispersion des données par rapport à leur moyenne, en calculant la moyenne des écarts au carré entre chaque valeur et la moyenne. Elle indique à quel point les données s’éloignent, en moyenne, de leur centre.
• Formule :
• Pour une population (toutes les données) : σ2=∑(xi−μ)2N\sigma^2 = \frac{\sum (x_i - \mu)^2}{N}σ2=N∑(xi​−μ)2​

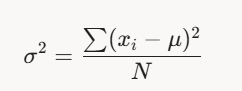
• • où xix_ixi​ est chaque valeur, μ\muμ est la moyenne de la population, et NNN est le nombre total de valeurs.
    • Pour un échantillon (sous-ensemble) : s2=∑(xi−xˉ)2n−1s^2 = \frac{\sum (x_i - \bar{x})^2}{n - 1}s2=n−1∑(xi​−xˉ)2​

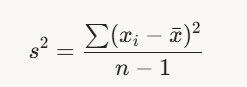
• • où xˉ\bar{x}xˉ est la moyenne de l’échantillon et nnn est le nombre de valeurs.

• Exemple : Données : 2, 4, 6 (moyenne = 4) :
  • Écarts : (2-4) = -2, (4-4) = 0, (6-4) = 2.
  • Écarts au carré : 4, 0, 4.
  • Variance (population) : (4 + 0 + 4) / 3 = 8 / 3 ≈ 2,67.
  • Variance (échantillon) : (4 + 0 + 4) / (3-1) = 8 / 2 = 4.
  • Utilité :
  • Fournit une mesure complète de la dispersion, en tenant compte de toutes les valeurs.
  • Base pour des analyses statistiques plus avancées (ex. tests d’hypothèses).
  • Limites :
  • Exprimée en unités au carré (ex. m² pour des mètres), ce qui la rend moins intuitive.
  • Sensible aux outliers, car les écarts sont amplifiés par le carré.
  3. Écart-type (Standard Deviation)
  • Définition : L’écart-type est la racine carrée de la variance. Il mesure la dispersion moyenne des données par rapport à la moyenne, dans les mêmes unités que les données d’origine.
  • Formule :
    • Pour une population : σ=σ2\sigma = \sqrt{\sigma^2}σ=σ2​.

• • • Pour un échantillon : s=s2s = \sqrt{s^2}s=s2​.

• • Exemple : Avec la variance précédente :
    • Population : σ=2,67≈1,63\sigma = \sqrt{2,67} \approx 1,63σ=2,67​≈1,63.

• • • Échantillon : s=4=2s = \sqrt{4} = 2s=4​=2. 

• • Utilité :
    • • Plus intuitif que la variance, car il est dans les mêmes unités que les données (ex. mètres, euros).
      • Permet de comprendre la "distance typique" des valeurs par rapport à la moyenne.
      • Très utilisé dans les distributions normales (ex. 68 % des données dans ±1 écart-type).
    • Limites :
      • Comme la variance, il est sensible aux valeurs extrêmes.
      • Moins informatif seul pour des distributions très asymétriques.

Comparaison

Exemple pratique

Données : 10, 12, 15, 20, 50 (moyenne = 21,4) :

• Étendue : 50 - 10 = 40.
• Variance (échantillon) :
  Écarts : -11,4, -9,4, -6,4, -1,4, 28,6 → au carré : 129,96, 88,36, 40,96, 1,96, 817,96 → somme = 1079,2 → s²=1079,2/4=269,8

Écart-type (échantillon) : s=269,8≈16,42s = \sqrt{269,8} \approx 16,42s=269,8​≈16,42.   

Interprétation :

• L’étendue (40) montre une grande amplitude, mais ne dit rien sur la répartition.
• L’écart-type (16,42) indique que les données s’écartent en moyenne de 16,42 unités de la moyenne, influencé par le 50.

En résumé

• Étendue : Une mesure brute et rapide, mais limitée.
• Variance : Une vue détaillée de la dispersion, mais moins pratique à interpréter seule.
• Écart-type : La mesure la plus courante et intuitive pour évaluer la variabilité. Ces trois outils se complètent pour donner une image complète de la dispersion des données !