Les mesures de tendance centrale sont des outils statistiques utilisés pour résumer un ensemble de données en identifiant une valeur "typique" ou "centrale". Les trois principales sont la moyenne, la médiane et le mode. Voici une explication détaillée de chacune, avec leurs définitions, calculs, utilités et limites :
- Moyenne (ou moyenne arithmétique)
- Définition : C’est la somme de toutes les valeurs d’un ensemble divisée par le nombre de valeurs. Elle représente le "point d’équilibre" des données.
- Formule : Moyenne=∑xin\text{Moyenne} = \frac{\sum x_i}{n}Moyenne=n∑xi
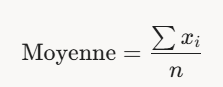
où xix_ixi est chaque valeur et nnn est le nombre total de valeurs.
- Exemple : Pour les notes 12, 15, 18, 10 : Moyenne=12+15+18+104=554=13,75\text{Moyenne} = \frac{12 + 15 + 18 + 10}{4} = \frac{55}{4} = 13,75Moyenne=412+15+18+10=455=13,75
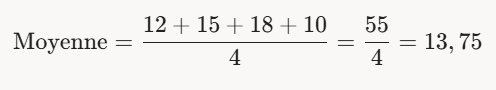
- Utilité :
- Donne une vue d’ensemble rapide.
- Très utilisée pour les données quantitatives continues ou discrètes (ex. salaires, températures).
- Limites :
- Sensible aux valeurs extrêmes (outliers). Exemple : Si on ajoute une note de 0 au jeu précédent, la moyenne tombe à 11.
- Peu pertinente pour les données qualitatives ordinales (ex. "bon/moyen/mauvais").
- Médiane
- Définition : C’est la valeur qui se trouve au milieu d’un ensemble de données triées par ordre croissant ou décroissant. Elle divise les données en deux moitiés égales (50 % en dessous, 50 % au-dessus).
- Calcul :
- Trier les valeurs.
- Si le nombre de valeurs (nnn) est impair, la médiane est la valeur centrale.
- Si nnn est pair, la médiane est la moyenne des deux valeurs centrales.
- Exemple :
- Supposons qu’un champion de course effectue une course d’entraînement typique de 200 mètres dans les temps suivants : 26,1 secondes, 25,6 secondes, 25,7 secondes, 25,2 secondes, 25,0 secondes, 27,8 secondes et 24,1 secondes. Comment calcule-t-on le temps médian?
| Rang | Temps (en secondes) |
| 1 | 24,1 |
| 2 | 25,0 |
| 3 | 25,2 |
| 4 | 25,6 |
| 5 | 25,7 |
| 6 | 26,1 |
| 7 | 27,8 |
- Il y a n = 7 valeurs, un nombre impair. La médiane correspondra donc à la valeur de rang
(n+1) ÷ 2 = (7 +1) ÷ 2 = 4
Le temps médian est de 25,6 secondes.
- Utilité :
- Résistante aux valeurs extrêmes, donc idéale pour des données asymétriques (ex. revenus avec quelques millionnaires).
- Représente mieux la tendance centrale en cas de distribution asymétrique
- Fonctionne aussi avec des données ordinales (ex. classements).
- Limites :
- Nécessite de trier les données, ce qui peut être long pour de grands ensembles.
- Moins informative que la moyenne sur la répartition globale.
- Mode
- Définition : C’est la valeur (ou les valeurs) qui apparaît le plus souvent dans un ensemble de données. Il représente la fréquence maximale.
- Calcul : Identifier la valeur la plus fréquente.
- Exemple :
- Données : 10, 12, 12, 15, 18 → Mode = 12 (apparaît 2 fois).
- Données : 5, 5, 8, 8, 10 → Mode = 5 et 8 (bimodal).
- Données : 3, 4, 5, 6 → Pas de mode (toutes apparaissent une fois).
- Cas particuliers :
- Unimodal : Un seul mode (ex : 18 est le seul mode)
- Bimodal : Deux modes (ex : si 14 et 18 apparaissent le même nombre de fois)
- Multimodal : Plusieurs modes
- Utilité :
- Fonctionne pour les données qualitatives et quantitatives
- Utile pour repérer la valeur la plus fréquente (valeur dominante).
- Limites :
- Peut ne pas exister (pas de répétition) ou être multiple (plusieurs modes).
- Ne donne aucune information sur la répartition ou la centralité des autres valeurs.
Comparaison et interprétation
|
Mesure |
Quand l’utiliser ? |
Avantage |
Inconvénient |
|
Moyenne |
Données quantitatives sans extrêmes |
Résume toutes les valeurs |
Sensible aux outliers |
|
Médiane |
Données avec outliers ou asymétriques |
Robuste aux extrêmes |
Ignore les valeurs extrêmes |
|
Mode |
Données qualitatives ou fréquences marquées |
Simple et intuitif |
Peu informatif seul |
Exemple concret
Imaginons les salaires d’un petit groupe : 2000, 2100, 2200, 2300, 50000 €.
- Moyenne : (2000 + 2100 + 2200 + 2300 + 50000) / 5 = 11 720 € → Influencée par le 50 000 €, peu représentative.
- Médiane : Tri : 2000, 2100, 2200, 2300, 50000 → Médiane = 2200 € → Plus proche de la réalité pour la majorité.
- Mode : Pas de mode (aucune répétition).
En résumé
- La moyenne donne une idée globale mais peut être trompeuse avec des outliers.
- La médiane offre une vue robuste du centre, idéale pour les données déséquilibrées.
- Le mode met en lumière les valeurs les plus courantes, parfait pour les catégories. Ces trois mesures se complètent et leur choix dépend du type de données et de l’objectif de l’analyse !
